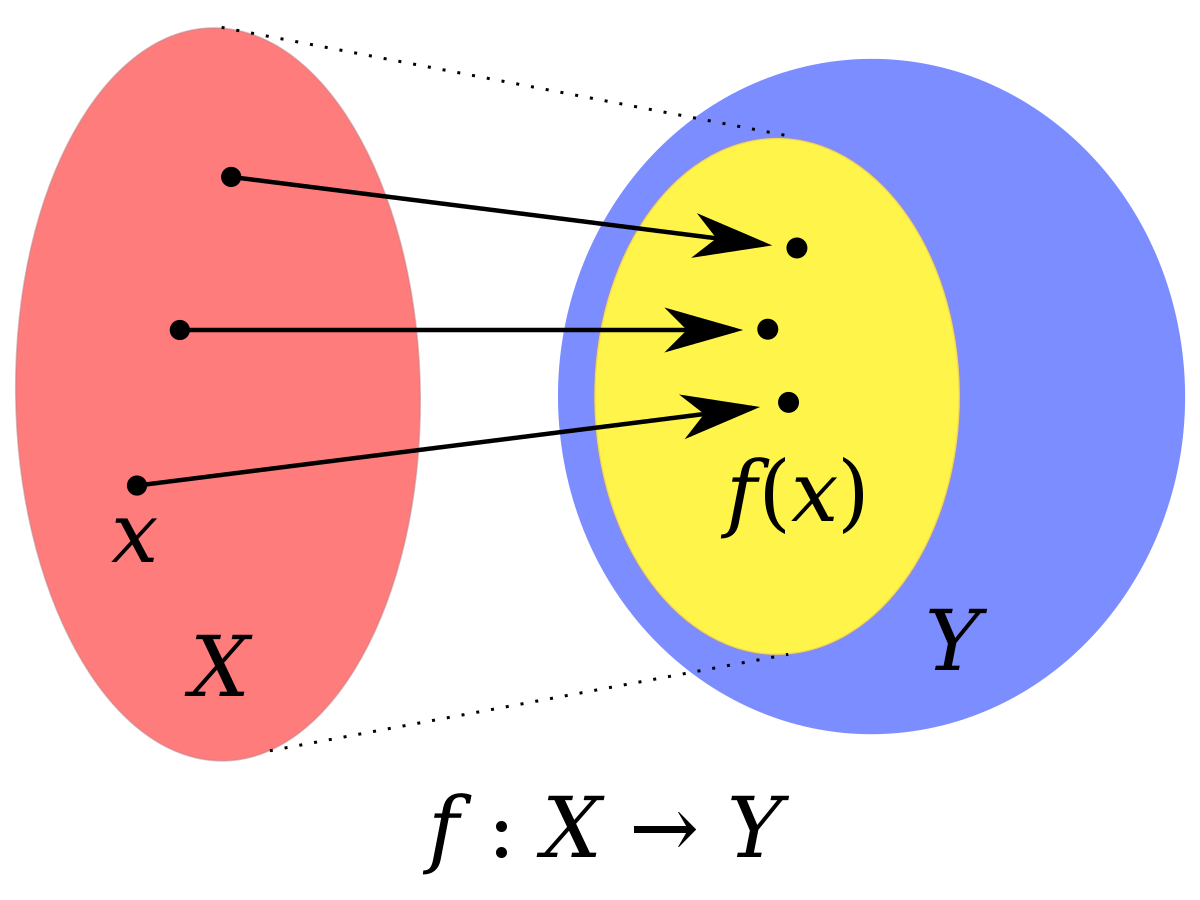
A function is a machine. We observe the world and wonder what generated the phenomena we see. Water flowing, a bicycle rolling, a tree growing. What we would need to put into the world in order to obtain what we observe? A function mathematizes the process, which is to say that it allows for careful descriptions of the inputs and outputs—descriptions for which there is no ambiguity, and thus descriptions that can be communicated without distortion of information. The allowable set of inputs is called the domain, the feasible set of outputs the range.
To think in terms in functions is to imagine the design of a machine that would be needed to convert a given set of inputs into a given set of outputs. To specify a function is to discover the machine that generated an observed outcome, which then allows us to ask what other inputs could be inserted into the machine, and what outputs would result. Or we can start with the inputs: if we restrict ourselves to a given set of inputs, what kind of machines can accommodate those inputs, and what can they produce? Or we can start in the middle with a machine that already exists—or one of our own design—and ask what it can do.
We can also create a sequence of machines. A second machine can use the outputs of a first machine as its own inputs. This is called composition.
Or we can build a machine that takes the outputs of the first machine and then converts them back into the original inputs. This is called an inverse function.
Polynomials are a certain class of very flexible, powerful machines. They can be used to produce a wide diversity of outputs, and are able to handle the kinds of inputs we can measure (integers, for examples, or fractions, or other easily measured amounts). Their machinery is both simple and exhaustive of the basic operations of mathematics: addition, subtraction (which is just addition in reverse), multiplication (which is just repeated addition), division (which is just multiplication in reverse), and exponentiation (which is just repeated multiplication).
The only threat is division by zero, which yields the absurdities of infinity.